Cet argument n’est pas simplement sorti de nulle part. Ce qui est impliqué peut être exprimé de diverses manières en termes de probabilités mathématiques. Pour cela, cependant, j’ai dû demander l’aide de mon frère, David M. Hodges, qui a obtenu son B.S. du Wheaton College en 1957, avec une majeure en mathématiques. Son expérience subséquente dans le domaine statistique comprend le service au dépôt de l’armée de Letterkenny (Pennsylvanie) en tant qu’officier statistique pour l’Agence de données sur les éléments majeurs de l’armée américaine et en tant que statisticien d’enquête de supervision pour le bureau local des manuels d’équipement du commandement du matériel de l’armée (1963-1967), et de 1967 à 1970 en tant que statisticien au quartier général du commandement du matériel de l’armée américaine. Washington, D.C. En 1972, il a obtenu une maîtrise en recherche opérationnelle de l’Université George Washington.
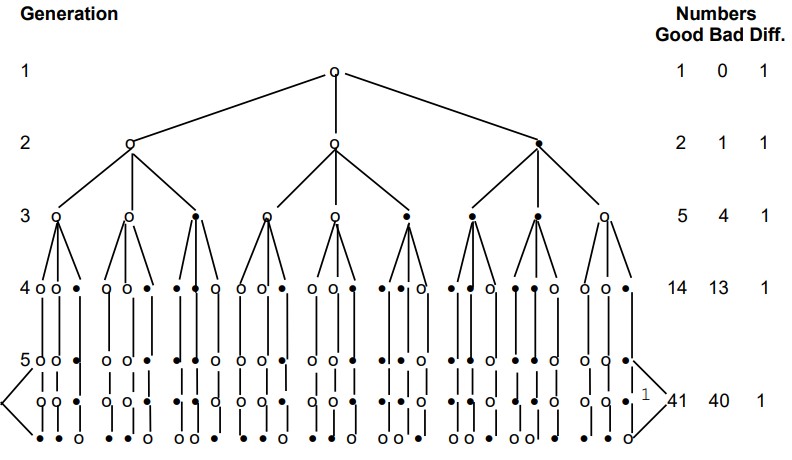
Vous trouverez ci-dessous un schéma d’une situation de transmission dans laquelle l’une des trois copies de l’autographe contient une erreur, tandis que deux conservent la lecture correcte. Par la suite, le phénomène textuel connu sous le nom de « mélange » entre en jeu, avec pour résultat que des lectures erronées sont introduites dans les bons manuscrits, ainsi que le processus inverse dans lequel les bonnes lectures sont introduites dans les mauvais. La déclaration de mon frère sur les probabilités de la situation suit le schéma dans ses propres mots. [Le schéma se trouve à la page suivante.]
À condition que les bons manuscrits et les mauvais manuscrits soient copiés un nombre égal de fois, et que la probabilité d’introduire une mauvaise lecture dans une copie faite à partir d’un bon manuscrit soit égale à la probabilité ou de réinsérer une bonne lecture dans une copie faite à partir d’un mauvais manuscrit, la lecture correcte prédominerait dans n’importe quelle génération de manuscrits. Le degré de prédominance de la bonne lecture dépend de la probabilité d’introduction de l’erreur.
Pour les besoins de la démonstration, nous appellerons l’autographe la première génération. Les copies de l’autographe seront appelées la deuxième génération. Les copies des manuscrits de la deuxième génération seront appelées la troisième génération et ainsi de suite. Le numéro de génération sera identifié par « n ». Par conséquent, dans la deuxième génération, n = 2.
*Numbers Good Bad Diff = Nombres Bon Mauvais Diff.

1 [N.B. — la cinquième génération est représentée par les trois lignes, c’est-à-dire que chaque manuscrit de la quatrième génération a été copié trois fois, comme dans les autres générations.]
En supposant que chaque manuscrit est copié un nombre égal de fois, le nombre de manuscrits produits dans une génération est kn-1, où « k » est le nombre de copies faites à partir de chaque manuscrit.
La probabilité que nous reproduisions une bonne lecture à partir d’un bon manuscrit est exprimée par « p » et la probabilité que nous introduisions une lecture erronée dans un bon manuscrit est « q ». La somme de p et q est égale à 1. Sur la base de nos dispositions originales, la probabilité de réinsérer une bonne lecture à partir d’un mauvais manuscrit est q et la probabilité de perpétuer une mauvaise lecture est P.
Le nombre attendu de bons manuscrits dans n’importe quelle génération est la quantité pkGn-1 + qkBn-1 et le nombre attendu de mauvais manuscrits est la quantité pkBn-1 + qkGn-1, où Gn-1 est le nombre de bons manuscrits à partir desquels nous copions et Bn-1 est le nombre de mauvais manuscrits à partir desquels nous copions. Le nombre de bons manuscrits produits dans une génération est Gn et le nombre de mauvais manuscrits produits est Bn. Nous avons donc les formules suivantes :
(1) Gn = pkGn-1 + qkBn-1 et
(2) Bn = pkBn-1 + qkGn-1 et
(3) kn-1 = Gn + Bn = pkGn-1 + qkBn-1 + pkBn-1 + qkGn-1.
Si Gn = Bn, alors pkGn-1 = qkBn-1 = pkBn-1 + qkGn-1 et pkGn-1 + qkBn-1 - pkBn-1 - qkGn-1 = 0.
En rassemblant des termes similaires, nous avons pkGn-1 - qkGn-1 + qkBn-1 - pkBn-1 = 0 et puisque k peut être factorisé, nous avons (p-q)Gn-1 + (q-p)Bn-1 = 0 et (p-q)Gn-1 - (p-q)Bn-1 = 0 et (p-q)(Gn-1 - Bn-1 ) = 0. Étant donné que l’expression de gauche est égale à zéro, soit (p-q) soit (Gn-1 - Bn-1 ) doit être égale à zéro. Mais (Gn-1 - Bn-1) ne peut pas être égal à zéro, puisque l’autographe était bon. Cela signifie que (p-q) doit être égal à zéro. En d’autres termes, le nombre attendu de mauvaises copies ne peut être égal au nombre attendu de bonnes copies que si la probabilité de faire une mauvaise copie est égale à la probabilité de faire une bonne copie.
Si Bn est supérieur à Gn, alors pkBn-1 + qkGn-1 > pkGn-1 + qkBn-1. Nous pouvons soustraire une quantité équivalente des deux côtés de l’inégalité sans changer l’inégalité. Ainsi, nous avons pkBn-1 + qkGn-1 - pkGn.1 -qkBn-1 > 0 et nous pouvons également diviser k en deux côtés en obtenant pBn-1 + qGn-1 - pGn-1 - qBn-1 > 0. Ensuite, (p-q)Bn-1 + (q-p)Gn-1 > 0. Aussi, (p-q)Bn-1 - (p-q)Gn-1 > 0. Aussi (p-q)(Bn.1 - Gn-1) > 0. Cependant, Gn-1 est supérieur à Bn-1 puisque l’autographe était bon. Par conséquent, (Bn-1 - Gn-1) < 0. Par conséquent, (p-q) doit également être inférieur à zéro. Cela signifie que q doit être supérieur à p pour que le nombre attendu de mauvais manuscrits soit supérieur au nombre attendu de bons manuscrits. Cela signifie également que la probabilité d’erreur doit être supérieure à la probabilité d’une copie correcte.
Le nombre attendu est en fait la moyenne de la loi binomiale. Dans la distribution binomiale, l’un des deux résultats suivants se produit ; soit un succès, c’est-à-dire une copie exacte, soit un échec, c’est-à-dire une copie inexacte.
Dans la situation discutée, l’équilibre s’installe lorsqu’une erreur est introduite. C’est-à-dire que la différence numérique entre le nombre de bonnes et de mauvaises copies est maintenue, une fois qu’une erreur a été introduite. En d’autres termes, les mauvaises copies sont rendues bonnes au même rythme que les bonnes copies sont rendues mauvaises. L’élément critique est la rapidité d’apparition d’une mauvaise copie. Par exemple, supposons que l’on fasse deux copies de chaque manuscrit et que q soit 25% ou 1/4. A partir de l’autographe, deux copies sont faites. La probabilité que la copie numéro 1 soit bonne est de 3/4, comme c’est le cas pour la deuxième copie. La probabilité que les deux soient bons est de 9/16 ou 56%. La probabilité que les deux soient mauvais est 1/4X1/4 ou 1/16 ou 6%. La probabilité que l’on soit mauvais est ¾ x ¼ + ¼ x ¾ ou 6/16 ou 38%. Le nombre attendu de bonnes copies est pkGn-1 + qkBn-1 qui est ¾ x 2 x 1 + ¼ x 2 x 0 ou 1,5. Le nombre attendu de mauvaises copies est de 2 - 1,5 ou 0,5. Or, si une erreur est introduite dans la seconde génération, le nombre des bonnes et des mauvaises copies sera, par la suite, égal. Mais la probabilité que cela se produise est de 44 %. Si la probabilité d’une copie exacte était supérieure à ¾, la probabilité d’une erreur dans la deuxième génération diminuerait. Il en va de même quel que soit le nombre de copies et le nombre de générations, tant que le nombre de copies faites à partir de mauvais manuscrits et le nombre de bons manuscrits sont égaux. Évidemment, si un type de manuscrit est copié plus fréquemment que l’autre, le type de manuscrit copié le plus fréquemment perpétuera sa lecture plus fréquemment.
Une autre observation est que si la probabilité d’introduire une lecture incorrecte diffère de la probabilité de réintroduire une lecture correcte, la discussion ne s’applique pas.
Cette discussion, cependant, n’est en aucun cas en faveur du point de vue que nous présentons. C’est l’inverse qui se produit. Une autre déclaration de mon frère clarifiera ce point.
Puisque la lecture correcte est la lecture apparaissant dans la majorité des textes de chaque génération, il est évident que, si un scribe consulte d’autres textes au hasard, la lecture majoritaire prédominera dans les sources consultées au hasard. Le rapport entre les bons textes consultés et les mauvais se rapprochera du rapport entre les bons et les mauvais textes des générations précédentes. Si un petit nombre de textes sont consultés, il se peut bien sûr qu’il n’y ait pas de ratio représentatif. Mais, dans un grand nombre de consultations de textes existants, l’approximation sera représentative du ratio existant dans tous les textes existants.
Dans la pratique, cependant, il n’y a probablement pas eu de comparaisons aléatoires. Le scribe consultait les textes qui lui étaient les plus facilement accessibles. En conséquence, il y aurait des branches de textes qui seraient corrompues parce que la majorité des textes disponibles pour le scribe contiendraient l’erreur. D’autre part, lorsqu’une erreur se produit pour la première fois, si le scribe vérifie plus d’un manuscrit, il trouvera toutes les lectures correctes, à l’exception de la copie qui a introduit l’erreur. Ainsi, lorsqu’un scribe utilise plus d’un manuscrit, la probabilité de reproduire une erreur est moindre que la probabilité d’introduire une erreur. Cela s’appliquerait à la génération qui suit immédiatement l’introduction d’une erreur.
Bref, notre problème théorique met donc en place des conditions de reproduction d’une erreur un peu trop favorables à l’erreur. Pourtant, même ainsi, dans cette situation idéalisée, la majorité initiale en faveur d’une lecture correcte a plus de chances d’être conservée que perdue. Mais la majorité de la cinquième génération est mince de 41 :40. Que dirons-nous, alors, lorsque nous rencontrerons la situation actuelle où (sur 100 manuscrits donnés) nous pouvons nous attendre à trouver un rapport de, disons, 80 :20 ? Il apparaît immédiatement que la probabilité que les 20 représentent la lecture originale dans n’importe quel type de situation de transmission normale est en effet faible.
Par conséquent, en abordant la question de ce point de vue (c’est-à-dire en commençant par les manuscrits existants), nous pouvons émettre l’hypothèse d’un problème impliquant (pour des raisons de commodité mathématique) 500 manuscrits existants dans lesquels nous avons des proportions de 75% à 25%. La déclaration de mon frère à ce sujet est la suivante :
Sur une base d’environ 500 manuscrits, dont 75 % montrent une lecture et 25 % une autre, étant donné une probabilité d’un tiers d’introduire une erreur, étant donné la même probabilité de corriger une erreur, et étant donné que chaque manuscrit est copié deux fois, la probabilité que la lecture majoritaire provienne d’une erreur est inférieure à une sur dix. Si la probabilité d’introduire une erreur est inférieure à un tiers, la probabilité que la lecture erronée se produise dans 75 % des cas est encore plus faible. Il en va de même si trois copies au lieu de deux sont faites à partir de chaque manuscrit. Par conséquent, la conclusion est que, compte tenu des conditions décrites, il est hautement improbable que la lecture erronée prédomine dans la mesure où le texte majoritaire prédomine.
Cette discussion s’applique à une lecture individuelle et ne doit pas être interprétée comme une déclaration de probabilité que les manuscrits copiés soient exempts d’erreurs. Il convient également de noter qu’une probabilité d’erreur d’un tiers est plutôt élevée, si un travail minutieux est impliqué.
Il ne suffira pas d’argumenter pour réfuter cette démonstration que, bien sûr, une erreur peut facilement être copiée plus souvent que la lecture originale dans un cas particulier. Naturellement, c’est vrai, et on l’admet volontiers. Mais le problème est plus aigu que cela. Si, par exemple, dans un certain livre du Nouveau Testament, nous trouvons (disons) 100 lectures où les manuscrits se divisent de 80 à 20 %, devons-nous supposer que dans chacun de ces cas, ou même dans la plupart d’entre eux, ce renversement des probabilités s’est produit ? C’est pourtant ce que dit, en effet, la critique textuelle contemporaine. Pour la majorité, le texte est rejeté à plusieurs reprises en faveur de lectures minoritaires. Il est donc évident que ce que les critiques textuels modernes affirment réellement – implicitement ou explicitement – ne constitue rien de moins qu’un rejet en bloc des probabilités à grande échelle !
Il est donc évident que ceux qui préfèrent de manière répétée et constante les lectures minoritaires aux lectures majoritaires – surtout lorsque les majorités rejetées sont très importantes – sont confrontés à un problème. Comment cette préférence peut-elle être justifiée par rapport aux probabilités latentes dans toute vision raisonnable de l’histoire de la transmission du Nouveau Testament ? Pourquoi devrions-nous rejeter ces probabilités ? Quel genre de phénomène textuel faudrait-il pour produire un texte majoritaire diffusé dans 80 % de la tradition, qui est pourtant plus souvent erroné que les 20 % qui s’y opposent ? Et si nous pouvions conceptualiser un tel phénomène textuel, quelle preuve y a-t-il qu’il ait jamais eu lieu ? Quelqu’un peut-il, logiquement, procéder à une critique textuelle sans fournir une réponse convaincante à ces questions ?
J’insiste depuis un certain temps sur le fait que le véritable nœud du problème textuel est de savoir comment expliquer la prépondérance écrasante du texte majoritaire dans la tradition existante. Les explications actuelles sur son origine sont sérieusement insuffisantes (voir ci-dessous sous Objections »). D’autre part, la proposition selon laquelle le texte majoritaire est le résultat naturel des processus normaux de transmission des manuscrits en donne une explication parfaitement naturelle. Les formes textuelles minoritaires sont ainsi expliquées, mutatis mutandis, comme existant sous leur forme minoritaire en raison de leur éloignement relatif du texte original. La théorie est simple mais, je crois, tout à fait adéquate à tous les niveaux. Son adéquation peut être démontrée aussi par la simplicité des réponses qu’il offre aux objections formulées contre lui. Voici quelques-unes de ces objections.