Aujourd’hui, toute la question de la dérivation des « types de textes» à travers des recensions historiques définies est ouverte au débat. En effet, E.C. Colwell, l’un des principaux critiques contemporains [1975], affirme dogmatiquement que la recension dite « syrienne » (telle que Hort l’aurait conçue) n’a jamais eu lieu. 2 Au lieu de cela, il insiste sur le fait que tous les types de texte sont le résultat d’un « processus » plutôt que d’une activité éditoriale définitive. 3 Tous les érudits ne seraient peut-être pas d’accord avec cette position, mais il est probablement juste de dire que peu d’entre eux seraient prêts à la nier catégoriquement. Au moins, la position de Colwell, dans la mesure où elle va, aurait beaucoup plu au grand antagoniste de Hort, Dean Burgon. Burgon, qui défendait le Textus Receptus avec un peu plus de véhémence que les érudits ne le souhaitent généralement, avait méprisé l’idée de la révision « syrienne », qui était la clé de voûte de la théorie de Westcott et Hort. D’ailleurs, l’idée a également été critiquée par d’autres, et un spécialiste des textes aussi connu que Sir Frederic Kenyon l’a officiellement abandonnée. 4 Mais la dissidence tendait à s’éteindre, et la forme sous laquelle elle existe aujourd’hui est tout à fait indépendante de la question de la valeur de la TR. En un mot, le scepticisme moderne à l’égard du concept classique de recensions prospère dans un nouveau contexte (en grande partie créé par les papyrus). Mais ce contexte n’est nullement décourageant pour ceux qui estiment que le Textus Receptus a été abandonné trop hâtivement.
1 Cet appendice est un résumé édité de « A Defense of the Majority-Text » par Zane C. Hodges et David M. Hodges (notes de cours non publiées, Dallas Theological Seminary, 1975) utilisé avec la permission des auteurs.
2 Sa déclaration est la suivante : « La Vulgate grecque – le type de texte byzantin ou alpha – n’a pas eu son origine dans un foyer aussi unique que le latin l’avait chez Jérôme » (italiques dans l’original). E.C.Colwell, « L’origine des types de texte des manuscrits du Nouveau Testament », Early Christian Origins, p.137.
3 Ibid., p. 136. Cf. notre discussion de ce point de vue sous Objections.
4 Cf. F.G. Kenyon, Manuel de la critique textuelle du Nouveau Testament, pp. 324 et suiv.
L’existence même de la discussion moderne sur l’origine des types de texte sert à mettre en relief ce que les défenseurs du texte reçu ont toujours soutenu. Leur argument était le suivant : Westcott et Hort n’ont pas réussi, par leur théorie des recensions, à expliquer adéquatement l’état réel de la tradition manuscrite grecque ; et en particulier, ils n’ont pas réussi à expliquer l’uniformité relative de cette tradition. Cette affirmation trouve aujourd’hui un appui en raison des questions que l’étude moderne a été forcée de soulever. Le soupçon est bien avancé que le texte majoritaire (comme Aland désigne la soi-disant famille byzantine 5) ne peut pas être retracé avec succès à un seul, même dans l’histoire textuelle. Mais, si ce n’est pas le cas, comment l’expliquer ?
5 Kurt Aland, « L’importance des papyrus pour le progrès de la recherche sur le Nouveau Testament », La Bible dans l’érudition moderne, p. 342. C’est le nom le plus scientifiquement non contestable jamais donné à cette forme de texte.
C’est là que réside la question cruciale sur laquelle toute théorie textuelle s’articule logiquement. Des études menées à l’Institut für neutestamentliche Textforschung de Münster (où des photos ou des microfilms de plus de 4 500 manuscrits ont déjà été collectés) tendent à soutenir l’opinion générale selon laquelle 90 [95] % des manuscrits cursifs grecs (minuscules) existants présentent sensiblement la même forme de texte.6 Si l’on considère les manuscrits sur papyrus et les manuscrits onciaux (majuscules) avec les cursives, le pourcentage de textes existants reflétant la forme majoritaire ne peut guère être inférieur à 80 [90] pour cent. Mais il s’agit d’un chiffre fantastiquement élevé et il faut absolument l’expliquer. En fait, en dehors d’une explication rationnelle d’une forme textuelle qui imprègne tout sauf 20 [10] pour cent de la tradition, personne ne devrait sérieusement prétendre savoir comment gérer nos matériaux textuels. Si l’on prétend qu’un grand progrès vers l’original est possible, alors que l’origine de 80 % des preuves grecques est enveloppée dans l’obscurité, une telle affirmation doit être considérée comme monstrueusement non scientifique, voire dangereusement obscurantiste. Aucun appel à des préférences subjectives pour telle ou telle lecture, tel texte ou tel texte, ne peut dissimuler ce fait. Le texte de la majorité doit être expliqué dans son ensemble, avant que ses affirmations dans leur ensemble puissent être rejetées scientifiquement.
6 Ibid., p. 344.
C’est la caractéristique particulière de la critique textuelle du Nouveau Testament que, parallèlement à une connaissance constamment accumulée de nos ressources manuscrites, il y a eu une diminution correspondante de la confiance avec laquelle l’histoire de ces sources est décrite. Le plan soigneusement élaboré de Westcott et Hort est maintenant considéré par tous les érudits réputés comme tout à fait inadéquat. L’affirmation confiante de Hort selon laquelle « il serait illusoire d’anticiper d’importants changements de texte à partir de toute acquisition de nouvelles preuves » est considérée à juste titre aujourd’hui comme extrêmement naïve. 7
7 Ibid., p. 330 et suiv.
La création de l’Institut für neutestamentliche Textforschung est pratiquement un effort pour tout recommencer à zéro en faisant ce qui aurait dû être fait en premier lieu, c’est-à-dire recueillir les preuves ! C’est dans ce contexte de réévaluation qu’il est tout à fait possible que la question fondamentale de l’origine du texte majoritaire s’impose sur le devant de la scène. En effet, on peut s’attendre à ce que si la critique moderne continue sa tendance vers des procédures plus authentiquement scientifiques, cette question redeviendra une considération centrale. Car elle reste la question la plus déterminante, logiquement, dans tout le domaine.
Les partisans du Textus Receptus ont-ils une explication à donner au texte majoritaire ? La réponse est oui. De plus, la position qu’ils maintiennent est si simple qu’elle est exempte des difficultés rencontrées par des hypothèses plus complexes. Il y a longtemps, alors qu’il attaquait l’autorité des nombres dans la critique textuelle, Hort a été contraint d’avouer : « Une présomption théorique subsiste en effet qu’une majorité de documents existants est plus susceptible de représenter une majorité de documents ancestraux à chaque étape de la transmission que l’inverse . » 8 En concédant cela, il ne faisait qu’affirmer un truisme de la transmission manuscrite. C’était le suivant : dans des circonstances normales, plus un texte est plus ancien que ses rivaux, plus grandes sont ses chances de survivre dans une pluralité ou une majorité des textes existants à une période ultérieure. Mais le texte le plus ancien de tous est l’autographe. Il faut donc tenir pour acquis qu’à moins d’une dislocation radicale dans l’histoire de la transmission, une majorité de textes aura beaucoup plus de chances de représenter correctement le caractère de l’original qu’une petite minorité de textes. Cela est particulièrement vrai lorsque le ratio est écrasant de 8 :2 [9 :1]. Dans des conditions de transmission raisonnablement normales, il serait pratiquement impossible, à toutes fins pratiques, qu’une forme de texte ultérieure garantisse une prépondérance aussi unilatérale de témoins existants. Même si nous repoussons l’origine du texte dit byzantin à une date contemporaine de P75 et Pss (vers 200) – une époque où il devait déjà y avoir des centaines de manuscrits – les proportions mathématiques telles que la tradition survivante révèle ne pourraient pas être expliquées en dehors de quelque bouleversement prodigieux dans l’histoire textuelle.
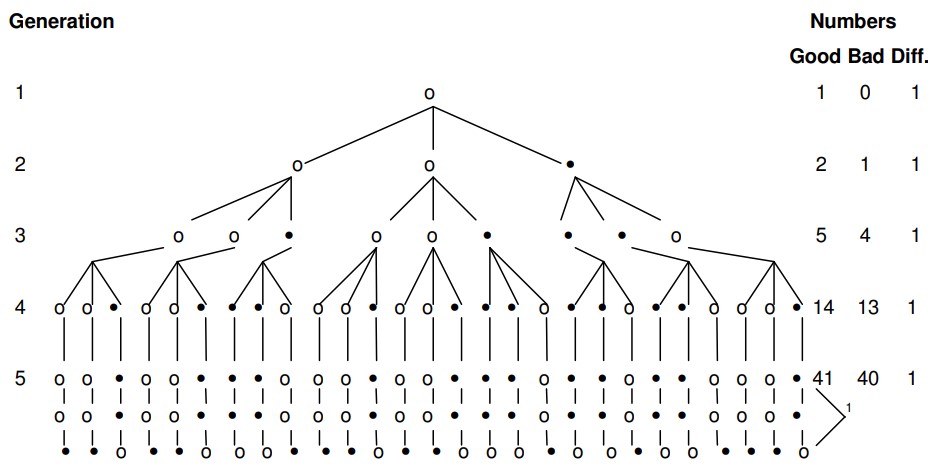
8 [N.B. : la cinquième génération est représentée par les trois lignes, c’est-à-dire que chaque manuscrit de la quatrième génération a été copié trois fois, comme dans les autres générations.]
Cet argument n’est pas simplement sorti de nulle part. Ce qui est impliqué peut être exprimé de diverses manières en termes de probabilités mathématiques. Pour cela, cependant, j’ai dû demander l’aide de mon frère, David M. Hodges, qui a obtenu son B.S. du Wheaton College en 1957, avec une majeure en mathématiques. Son expérience subséquente dans le domaine statistique comprend le service au dépôt de l’armée de Letterkenny (Pennsylvanie) en tant qu’officier statistique pour l’Agence de données sur les éléments majeurs de l’armée américaine et en tant que statisticien d’enquête de supervision pour le bureau local des manuels d’équipement du commandement du matériel de l’armée (1963-1967), et de 1967 à 1970 en tant que statisticien au quartier général du commandement du matériel de l’armée américaine. Washington, D.C. En 1972, il a obtenu une maîtrise en recherche opérationnelle de l’Université George Washington.
Vous trouverez ci-dessous un schéma d’une situation de transmission dans laquelle l’une des trois copies de l’autographe contient une erreur, tandis que deux conservent la lecture correcte. Par la suite, le phénomène textuel connu sous le nom de « mélange » entre en jeu, avec pour résultat que des lectures erronées sont introduites dans les bons manuscrits, ainsi que le processus inverse dans lequel les bonnes lectures sont introduites dans les mauvais. La déclaration de mon frère sur les probabilités de la situation suit le schéma dans ses propres mots.

*Generation = Génération / Numbers = Nombres / Good Bad Diff.= Bon Mauvais Diff.
À condition que les bons manuscrits et les mauvais manuscrits soient copiés un nombre égal de fois, et que la probabilité d’introduire une mauvaise lecture dans une copie faite à partir d’un bon manuscrit soit égale à la probabilité ou de réinsérer une bonne lecture dans une copie faite à partir d’un mauvais manuscrit, la lecture correcte prédominerait dans n’importe quelle génération de manuscrits. Le degré de prédominance de la bonne lecture dépend de la probabilité d’introduction de l’erreur.
Pour les besoins de la démonstration, nous appellerons l’autographe la première génération. Les copies de l’autographe seront appelées la deuxième génération. Les copies des manuscrits de la deuxième génération seront appelées la troisième génération et ainsi de suite. Le numéro de génération sera identifié par « n ». Par conséquent, dans la deuxième génération, n = 2.
En supposant que chaque manuscrit est copié un nombre égal de fois, le nombre de manuscrits produits dans une génération est kn-1, où « k » est le nombre de copies faites à partir de chaque manuscrit.
La probabilité que nous reproduisions une bonne lecture à partir d’un bon manuscrit est exprimée par « p » et la probabilité que nous introduisions une lecture erronée dans un bon manuscrit est « q ». La somme de p et q est égale à 1. Sur la base de nos dispositions originales, la probabilité de réinsérer une bonne lecture à partir d’un mauvais manuscrit est q et la probabilité de perpétuer une mauvaise lecture est p.
Le nombre attendu de bons manuscrits dans n’importe quelle génération est la quantité pkGn-1 + qkBn-1 et le nombre attendu de mauvais manuscrits est la quantité pkBn-1 + qkGn-1, où Gn-1 est le nombre de bons manuscrits à partir desquels nous copions et Bn-1 est le nombre de mauvais manuscrits à partir desquels nous copions. Le nombre de bons manuscrits produits dans une génération est Gn et le nombre de mauvais manuscrits produits est Bn. Nous avons donc les formules suivantes :
(1) Gn = pkGn-1 + qkBn-1 et
(2) Bn = pkBn-1 + qkGn-1 et
(3) kn-1 = Gn + Bn = pkGn-1 + qkBn-1 + pkBn-1 + qkGn-1.
Si Gn = Bn, alors pkGn-1 = qkBn-1 = pkBn-1 + qkGn-1 et pkGn-1 + qkBn-1 - pkBn-1 - qkGn-1 = 0.
En rassemblant des termes similaires, nous avons pkGn-1 - qkGn-1 + qkBn-1 - pkBn-1 = 0 et puisque k peut être factorisé, nous avons (p-q)Gn-1 + (q-p)Bn-1 = 0 et (p-q)Gn-1 - (p-q)Bn-1 = 0 et (p-q)(Gn-1 - Bn-1) = 0. Puisque l’expression de gauche est égale à zéro, (p-q) ou (Gn-1 - Bn-1) doit être égal à zéro. Mais (Gn-1 - Bn-1) ne peut pas être égal à zéro, puisque l’autographe était bon. Cela signifie que (p-q) doit être égal à zéro. En d’autres termes, le nombre attendu de mauvaises copies ne peut être égal au nombre attendu de bonnes copies que si la probabilité de faire une mauvaise copie est égale à la probabilité de faire une bonne copie.
Si Bn est supérieur à Gn, alors pkBn-1 + qkGn-1 > pkGn-1 + qkBn-1. Nous pouvons soustraire une quantité équivalente des deux côtés de l’inégalité sans changer l’inégalité. Ainsi, on a pkBn-1 + qkGn-1 - pkGn-1 - qkBn-1 > 0 et on peut aussi diviser k en deux côtés en obtenant pBn-1 + qGn-1 - pGn-1 - qBn-1 > 0. Ensuite, (p-q)Bn.1 + (q-p)Gn-1 > 0. Aussi, (p-q)Bn-1 - (p-q)Gn-1 > 0. Aussi (p-q)(Bn-1 - Gn-1) > 0. Cependant, Gn-1 est supérieur à Bn-1 puisque l’autographe était bon. Par conséquent, (Bn-1 - Gn-1) < 0. Par conséquent, (p-q) doit également être inférieur à zéro. Cela signifie que q doit être supérieur à p pour que le nombre attendu de mauvais manuscrits soit supérieur au nombre attendu de bons manuscrits. Cela signifie également que la probabilité d’erreur doit être supérieure à la probabilité d’une copie correcte.
Le nombre attendu est en fait la moyenne de la loi binomiale. Dans la distribution binomiale, l’un des deux résultats suivants se produit ; soit un succès, c’est-à-dire une copie exacte, soit un échec, c’est-à-dire une copie inexacte.
Dans la situation discutée, l’équilibre s’installe lorsqu’une erreur est introduite. C’est-à-dire que la différence numérique entre le nombre de bonnes et de mauvaises copies est maintenue, une fois qu’une erreur a été introduite. En d’autres termes, les mauvaises copies sont rendues bonnes au même rythme que les bonnes copies sont rendues mauvaises. L’élément critique est la rapidité d’apparition d’une mauvaise copie. Par exemple, supposons que deux copies soient faites à partir de chaque manuscrit et que q soit 25% ou 1/4. À partir de l’autographe, deux copies sont faites. La probabilité que la copie numéro 1 soit bonne est de 3/4, comme c’est le cas pour la deuxième copie. La probabilité que les deux soient bons est de 9/16 ou 56%. La probabilité que les deux soient mauvais est de 1/4 x 1/4 ou 1/16 ou 6%. La probabilité que l’on soit mauvais est de 3/4 x 1/4 + 1/4 x 3/4 ou 6/16 ou 38%. Le nombre attendu de bonnes copies est pkGn-1 + qkBn-1 qui est 3/4 x 2 x 1 + 1/4x 2 x 0 ou 1,5. Le nombre attendu de mauvaises copies est de 2 - 1,5 ou 0,5. Or, si une erreur est introduite dans la seconde génération, le nombre des bonnes et des mauvaises copies sera, par la suite, égal. Mais la probabilité que cela se produise est de 44 %. Si la probabilité d’une copie exacte était supérieure à 3/4, la probabilité d’une erreur dans la deuxième génération diminuerait. Il en va de même quel que soit le nombre de copies et le nombre de générations, tant que le nombre de copies faites à partir de mauvais manuscrits et le nombre de bons manuscrits sont égaux. Évidemment, si un type de manuscrit est copié plus fréquemment que l’autre, le type de manuscrit copié le plus fréquemment perpétuera sa lecture plus fréquemment.
Une autre observation est que si la probabilité d’introduire une lecture incorrecte diffère de la probabilité de réintroduire une lecture correcte, la discussion ne s’applique pas.
Cette discussion, cependant, n’est en aucun cas en faveur du point de vue que nous présentons. C’est l’inverse qui se produit. Une autre déclaration de mon frère clarifiera ce point.
Puisque la lecture correcte est la lecture apparaissant dans la majorité des textes de chaque génération, il est évident que, si un scribe consulte d’autres textes au hasard, la lecture majoritaire prédominera dans les sources consultées au hasard. Le rapport entre les bons textes consultés et les mauvais se rapprochera du rapport entre les bons et les mauvais textes des générations précédentes. Si un petit nombre de textes sont consultés, il se peut bien sûr qu’il n’y ait pas de ratio représentatif. Mais, dans un grand nombre de consultations de textes existants, l’approximation sera représentative du ratio existant dans tous les textes existants.
Dans la pratique, cependant, il n’y a probablement pas eu de comparaisons aléatoires. Le scribe consultait les textes qui lui étaient les plus facilement accessibles. En conséquence, il y aurait des branches de textes qui seraient corrompues parce que la majorité des textes disponibles pour le scribe contiendraient l’erreur. D’autre part, lorsqu’une erreur se produit pour la première fois, si le scribe vérifie plus d’un manuscrit, il trouvera toutes les lectures correctes, à l’exception de la copie qui a introduit l’erreur. Ainsi, lorsqu’un scribe utilise plus d’un manuscrit, la probabilité de reproduire une erreur est moindre que la probabilité d’introduire une erreur. Cela s’appliquerait à la génération qui suit immédiatement l’introduction d’une erreur.
Bref, notre problème théorique met donc en place des conditions de reproduction d’une erreur un peu trop favorables à l’erreur. Pourtant, même ainsi, dans cette situation idéalisée, la majorité initiale en faveur d’une lecture correcte a plus de chances d’être conservée que perdue. Mais la majorité de la cinquième génération est mince de 41 :40. Que dirons-nous, alors, lorsque nous rencontrerons la situation actuelle où (sur 100 manuscrits donnés) nous pouvons nous attendre à trouver un rapport de, disons, 80 :20 ? Il apparaît immédiatement que la probabilité que les 20 représentent la lecture originale dans n’importe quel type de situation de transmission normale est en effet faible.
Par conséquent, en abordant la question de ce point de vue (c’est-à-dire en commençant par les manuscrits existants), nous pouvons émettre l’hypothèse d’un problème impliquant (pour des raisons de commodité mathématique) 500 manuscrits existants dans lesquels nous avons des proportions de 75% à 25%. La déclaration de mon frère à ce sujet est la suivante :
Sur environ 500 manuscrits, dont 75 % montrent une lecture et 25 % une autre, compte tenu d’une probabilité d’introduction et d’erreur d’un tiers, étant donné la même probabilité de corriger une erreur, et étant donné que chaque manuscrit est copié deux fois, la probabilité que la lecture majoritaire provienne d’une erreur est inférieure à une sur dix. Si la probabilité d’introduire une erreur est inférieure à un tiers, la probabilité que la lecture erronée se produise dans 75 % des cas est encore plus faible. Il en va de même si trois copies au lieu de deux sont faites à partir de chaque manuscrit. Par conséquent, la conclusion est que, compte tenu des conditions décrites, il est hautement improbable que la lecture erronée prédomine dans la mesure où le texte majoritaire prédomine.
Cette discussion s’applique à une lecture individuelle et ne doit pas être interprétée comme une déclaration de probabilité que les manuscrits copiés soient exempts d’erreurs. Il convient également de noter qu’une probabilité d’erreur d’un tiers est plutôt élevée, si un travail minutieux est impliqué.
Il ne suffira pas d’argumenter pour réfuter cette démonstration que, bien sûr, une erreur peut facilement être copiée plus souvent que la lecture originale dans un cas particulier. Naturellement, c’est vrai, et on l’admet volontiers. Mais le problème est plus aigu que cela. Si, par exemple, dans un certain livre du Nouveau Testament, nous trouvons (disons) 100 lectures où les manuscrits se divisent de 80 à 20 %, devons-nous supposer que dans chacun de ces cas, ou même dans la plupart d’entre eux, ce renversement des probabilités s’est produit ? C’est pourtant ce que dit, en effet, la critique textuelle contemporaine. Pour la majorité, le texte est rejeté à plusieurs reprises en faveur de lectures minoritaires. Il est donc évident que ce que les critiques textuels modernes affirment réellement – implicitement ou explicitement – ne constitue rien de moins qu’un rejet en bloc des probabilités à grande échelle !
Il est donc évident que ceux qui préfèrent systématiquement et systématiquement les lectures minoritaires aux lectures majoritaires – surtout lorsque les majorités rejetées sont très importantes – sont confrontés à un problème. Comment cette préférence peut-elle être justifiée par rapport aux probabilités latentes dans toute vision raisonnable de l’histoire de la transmission du Nouveau Testament ? Pourquoi devrions-nous rejeter ces probabilités ? Quel genre de phénomène textuel faudrait-il pour produire un texte majoritaire diffusé dans 80 % de la tradition, qui est pourtant plus souvent erroné que les 20 % qui s’y opposent ? Et si nous pouvions conceptualiser un tel phénomène textuel, quelle preuve y a-t-il qu’il ait jamais eu lieu ? Quelqu’un peut-il, logiquement, procéder à une critique textuelle sans fournir une réponse convaincante à ces questions ?
J’insiste depuis un certain temps sur le fait que le véritable nœud du problème textuel est de savoir comment expliquer la prépondérance écrasante du texte majoritaire dans la tradition existante. Les explications actuelles sur son origine sont sérieusement insuffisantes (voir ci-dessous sous Objections »). D’autre part, la proposition selon laquelle le texte majoritaire est le résultat naturel des processus normaux de transmission des manuscrits en donne une explication parfaitement naturelle. Les formes textuelles minoritaires sont ainsi expliquées, mutatis mutandis, comme existant sous leur forme minoritaire en raison de leur éloignement relatif du texte original. La théorie est simple mais, je crois, tout à fait adéquate à tous les niveaux. Son adéquation peut être démontrée aussi par la simplicité des réponses qu’il offre aux objections formulées contre lui. Voici quelques-unes de ces objections.
1. Étant donné que tous les manuscrits ne sont pas copiés un nombre pair de fois, les démonstrations mathématiques comme celles ci-dessus ne sont pas valides.
Mais c’est mal comprendre le but de telles manifestations. Bien sûr, le schéma donné ci-dessus est une situation « idéalisée » qui ne représente pas ce qui s’est réellement passé. Au lieu de cela, cela montre simplement que toutes choses étant égales par ailleurs, la probabilité statistique favorise la perpétuation à chaque génération du statut de majorité originelle de la lecture authentique. Et il faut alors garder à l’esprit que plus la majorité initiale est grande, plus cet argument des probabilités devient convaincant. Développons ce point.
Si nous imaginons une tige comme suit
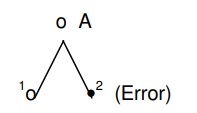
*(Erreur)
dans lequel A = autographe et (1) et (2) sont des copies faites à partir de celui-ci, il est évident que, dans l’abstrait, l’erreur de (2) a une chance égale de se perpétuer en nombre égal avec la lecture authentique de (1). Mais, bien sûr, en réalité , (2) peut être copié plus fréquemment que (1) et ainsi l’erreur se perpétue dans un plus grand nombre de manuscrits ultérieurs que la véritable lecture en (1).
Pour l’instant ça va. Mais supposons...
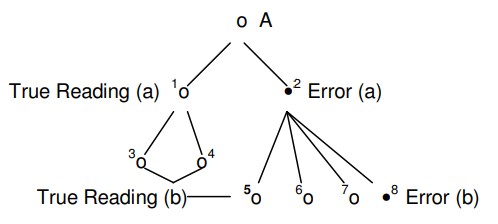
*True Reading (a) = Lecture vraie (a) / Error (a) = Erreur (a) / True Reading (b) = Lecture vraie (b) / Error (b) = Erreur (b) /
Maintenant, nous avons concédé que l’erreur désignée (a) se perpétue en plus grand nombre que la vraie lecture (a), de sorte que « l’erreur (a) » se trouve dans les copies 5-6-7-8, tandis que la « vraie lecture (a) » ne se trouve que dans les copies 3 et 4. Mais lorsque « l’erreur (b) » est introduite dans l’exemplaire 8, sa rivale (« lecture vraie (b) ») se trouve dans les exemplaires 3-4-5-6-7. 1 Quelqu’un supposera-t-il qu’à ce stade, il est probable que « l’erreur (b) » aura la même chance que « l’erreur (a) » et que le manuscrit 8 sera copié plus souvent que 3-4-5-6-7 combinés ?
Mais même en admettant cette situation beaucoup moins probable, supposons encore une fois...
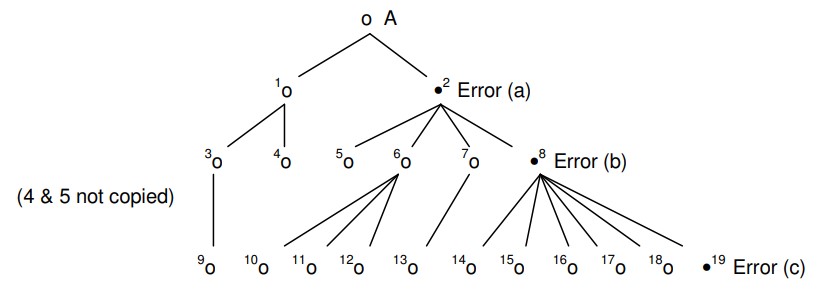
*(4 & 5 not copied) = (4 & 5 non copiés) /Error
=Erreur
Quelqu’un croira-t-il que les probabilités favorisent une répétition de la même situation pour « l’erreur (c) » dans la copie 19 ?
N’est-il pas évident qu’au fur et à mesure que les manuscrits se multiplient et que les erreurs s’introduisent plus loin dans le flux de transmission, la probabilité que l’erreur soit copiée plus fréquemment que le nombre de plus en plus grand de textes rivaux diminue considérablement ?
Ainsi, admettre que certaines erreurs pourraient être copiées plus fréquemment que la lecture concurrente et authentique ne touche en rien au cœur de notre argumentation. La raison en est simple : la critique moderne rejette de manière répétée et systématique les lectures majoritaires à très grande échelle. Mais, à chaque rejet de ce type, la probabilité que ce rejet soit valide est considérablement réduite. Renverser plusieurs fois les probabilités statistiques est une chose. Les renverser de manière répétée et persistante en est une autre !
Par « erreur (b) », nous entendons, bien sûr, une erreur commise à un autre endroit dans le texte transmis par l’autographe. Nous ne voulons pas dire que l'« erreur (b) » a été remplacée par « l’erreur (a) ». Par conséquent, alors que les copies 5-6-7 contiennent « l’erreur (a) », elles contiennent également la lecture autographe originale qui est la rivale de « l’erreur (b) ».
Par conséquent, nous continuons d’insister sur le fait que rejeter les lectures de texte majoritaires en grand nombre sans fournir une justification globale crédible pour cette procédure revient à aller aveuglément à l’encontre de toute probabilité raisonnable.
2. Le texte majoritaire peut être expliqué comme le résultat d’un « processus » qui a abouti à la formation progressive d’un type de texte numériquement prépondérant.
Le point de vue du « processus » du texte majoritaire semble gagner en faveur aujourd’hui parmi les érudits textuels du Nouveau Testament. Pourtant, à ma connaissance, personne n’a offert d’explication détaillée de ce qu’était exactement le processus, quand il a commencé, ou comment, une fois commencé, il a atteint le résultat revendiqué. En effet, les partisans du point de vue du « processus » sont probablement bien avisés de rester vagues à ce sujet parce que, à première vue, il semble impossible de concevoir un quelconque type de processus qui soit à la fois historiquement crédible et adéquat pour rendre compte de tous les faits. Il faut se rappeler que le texte de la majorité est relativement uniforme dans son caractère général, avec des variations relativement faibles entre ses principaux représentants. 9
9 Les mots clés ici sont « relativement » et « comparativement ». Naturellement, les membres individuels du texte majoritaire montrent des degrés variables de conformité à celui-ci. Néanmoins, la proximité de ses représentants par rapport à la norme générale n’est pas difficile à démontrer dans la plupart des cas. Par exemple, dans une étude portant sur une centaine de lieux de variation dans Jean 11, les représentants du texte majoritaire utilisé dans l’étude ont montré une fourchette d’accord allant d’environ 70 % à 93 %. Cf. Ernest C. Colwell et Ernest W. Tune, pp. 28,31. L’accord de 93 % du codex oncial Omega avec le Textus Receptus se compare bien à l’accord de 92 % trouvé entre P75 et B. L’affinité d’Omega avec le TR est plus typique du modèle que l’on trouverait dans la grande masse de textes minuscules. Des niveaux élevés d’accord de ce type sont (comme dans le cas de P75 et B) le résultat d’une base ancestrale partagée. Ce sont les divergences qui sont le résultat d’un « processus » et non l’inverse.
Un exposé plus général et sommaire de la question est fait par Epp : « [...] les manuscrits byzantins ensemble, après tout, forment un groupe assez soudé, et les variations en question au sein de l’ensemble de ce grand groupe sont relativement mineures. (Eldon Jay Epp, « La méthode du profil de Claremont pour regrouper les manuscrits minuscules du Nouveau Testament », p. 33.)
Personne n’a encore expliqué comment un long et lent processus s’étendant sur plusieurs siècles ainsi que sur une vaste zone géographique, et impliquant une multitude de copistes, qui souvent ne connaissaient rien de l’état du texte en dehors de leurs propres monastères ou scriptoria (salles destinées à faciliter la copie fidèle des manuscrits), a pu atteindre cette uniformité généralisée à partir de la diversité présentée par les formes antérieures du texte. Même une édition officielle du Nouveau Testament – promue avec la sanction ecclésiastique dans tout le monde connu – aurait eu beaucoup de mal à atteindre ce résultat, comme le démontre amplement l’histoire de la Vulgate de Jérôme. 10 Mais un processus non guidé qui parvient à une stabilité et à une uniformité relatives dans les circonstances textuelles, historiques et culturelles diversifiées dans lesquelles le Nouveau Testament a été copié, impose à notre imagination des contraintes impossibles.
10 Après avoir décrit les vicissitudes qui ont affecté la transmission de la Vulgate, Metzger conclut : « En conséquence, les plus de 8 000 manuscrits de la Vulgate qui existent aujourd’hui présentent la plus grande quantité de contamination croisée des types textuels. » (Texte du Nouveau Testament, p. 76.) L’uniformité du texte est toujours la plus grande à la source et diminue – plutôt qu’elle n’augmente – à mesure que la tradition s’étend et se multiplie. Cette mise en garde n’est pas prise en compte par le point de vue du « processus » du texte majoritaire.
Il semble donc que plus le point de vue du « processus » peut être formulé de façon claire et précise, plus il est susceptible d’être vulnérable à toutes les objections potentielles qui viennent d’être mentionnées. De plus, lorsqu’une telle vision sera exprimée, elle devra se situer définitivement quelque part dans l’histoire, avec de nombreux inconvénients supplémentaires pour ses défenseurs. Car, rappelons-le, tout comme l’histoire est silencieuse sur toute « recension syrienne » (comme celle imaginée par Hort), de même l’histoire est silencieuse sur tout type de « processus » qui influençait ou guidait d’une manière ou d’une autre les scribes lors de la transmission des manuscrits. Les critiques modernes sont les premiers à découvrir un tel « processus », mais avant de l’accepter, nous devrons avoir plus que des affirmations vagues et non documentées à son sujet.
Il ne semble pas injuste de dire que la tentative d’expliquer le texte majoritaire par un « processus » obscur et nébuleux est un aveu implicite de faiblesse de la part de la critique contemporaine. L’érosion du point de vue de Westcott et Hort, qui faisait remonter ce texte à une recension officielle et définitive du Nouveau Testament, a créé un vide très difficile à combler. Plus que jamais, semble-t-il, les critiques ne peuvent pas rejeter le texte de la majorité et en même temps l’expliquer. Et c’est là où nous voulons en venir ! Le rejet du texte de la majorité et l’explication crédible de ce texte sont tout à fait incompatibles l’un avec l’autre. Mais l’acceptation du texte majoritaire fournit immédiatement une explication de ce texte et des textes rivaux ! Et c’est l’essence même de la démarche scientifique que de préférer les hypothèses qui expliquent les faits disponibles à celles qui ne le font pas !